13 August 2021
PLEASE NOTE: The Viewpoints on our website are to be read and freely shared by all. If they are republished, the following text should be used: “This Viewpoint was originally published on the REVIVE website revive.gardp.org, an activity of the Global Antibiotic Research & Development Partnership (GARDP).”
The development of vaccines for COVID-19 has been a magnificent achievement. At least five of these vaccines have been trialled in various European countries or North America. Table 1 summarises the vaccines and their characteristics. For further reading, I recommend Comparing the COVID-19 Vaccines: How Are They Different? by Kathy Katella1. In this article, I shall discuss various statistical aspects of five large phase 3 trials used to support vaccine registration in order to learn what key aspects of their success could inform other fields such as antimicrobial R&D.
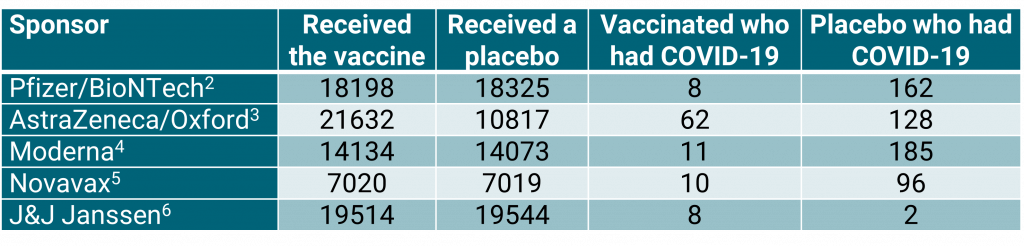
Table 1: Summary of results from five large vaccine studies.
The most important thing to note from table 1 is that four of the sponsors used a 1:1 allocation for vaccine to placebo. The exception is AstraZeneca/Oxford who used 2:1. It should also be noted that the J&J Janssen vaccine is administered as one dose; the others are administered as two doses.
The morals are clear. Be very cautious in accepting claims from observational studies. This applies not only to studies of vaccines for COVID-19 but more widely for studies of treatments of infections generally and, indeed, for all studies of treatment efficacy.
The efficacy of vaccines for COVID-19
Figure 1 is a graphical display showing estimated vaccine efficacy and the associated 95% confidence intervals for the five trials. Vaccine efficacy is calculated as a relative risk reduction as follows:
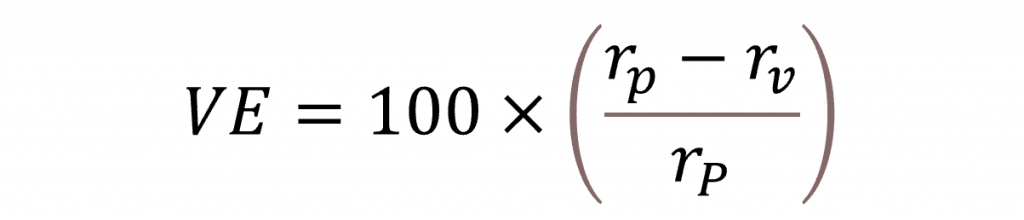
Here rp is the risk of catching COVID-19 if receiving the placebo and rv the corresponding risk if receiving the vaccine. The numerators to calculate these risks will be the numbers of cases receiving the placebo and vaccine, respectively, and the denominators will be ‘exposure’, either measured in terms of number of persons or person-years.
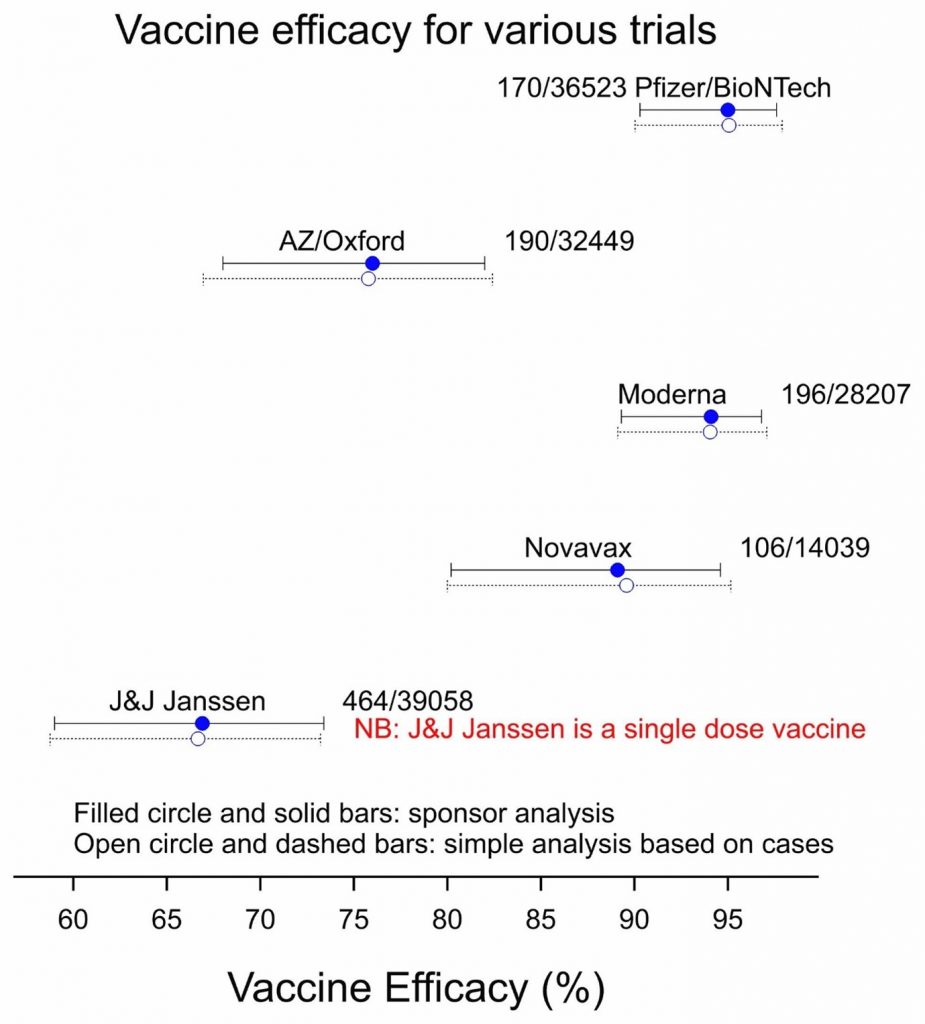
Figure 1: Vaccine efficacy for five vaccines based on the corresponding phase 3 trials. Total numbers of cases/subjects are indicated.
The sponsoring vaccine manufacturers may have made different choices for the denominator and will have adjusted for different covariates. In one case, the Pfizer/BioNTech vaccine, the analysis was Bayesian7, but in the other cases, it was frequentist. However, my analysis, which was frequentist, made use neither of any denominator nor of covariates. I simply considered what might be called the risk proportion, let us represent this by the risk of getting COVID-19 when given a vaccine as a proportion of the sum of the risks when given a vaccine or placebo. So, we have:

I then calculated exact confidence intervals for this proportion using cases and allocation ratio only and converted the results to the vaccine efficacy scale.
What is remarkable about this is how close my simple calculations are to the analyses carried out by the sponsors. There are various technical reasons for this, in particular, that a major source of uncertainty is the number of cases. Where numbers are small, so that the total numbers of subjects, which are large are unimportant in comparison as regards contribution to uncertainty. However, it is also a tribute to the value of concurrent control in these well-designed clinical trials.
Figure 2 shows the importance of concurrent control. This shows the estimated infection rate (the ratio of cases to subjects) when individuals are given a placebo and associated confidence intervals calculated in two different ways: using the binomial distribution, which I prefer because it is ‘exact’, and using the normal approximation, which lends itself to a formal summary of results using a so-called ‘meta-analysis’. The placebo risk seems to be very different from study to study and this is confirmed by the results of a meta-analysis.
What can be learnt from these trials?
The meta-analysis shows considerable evidence of heterogeneity, that is to say, the results vary more from trial to trial than can be explained by simple random variation. One plausible explanation is that infection rates have varied considerably from place to place and at different times. In consequence, the confidence interval for the random effects analysis is much wider than for the fixed-effects meta-analysis. The result is that if we were forced to use historical figures for judging the efficacy of a new vaccine, rather than concurrent controls, the estimate of efficacy and the estimate of the uncertainty of efficacy would be very unreliable. One might argue that this is to raise an unnecessary worry: no responsible sponsor would rely on controls of this sort and no regulator would accept this approach.
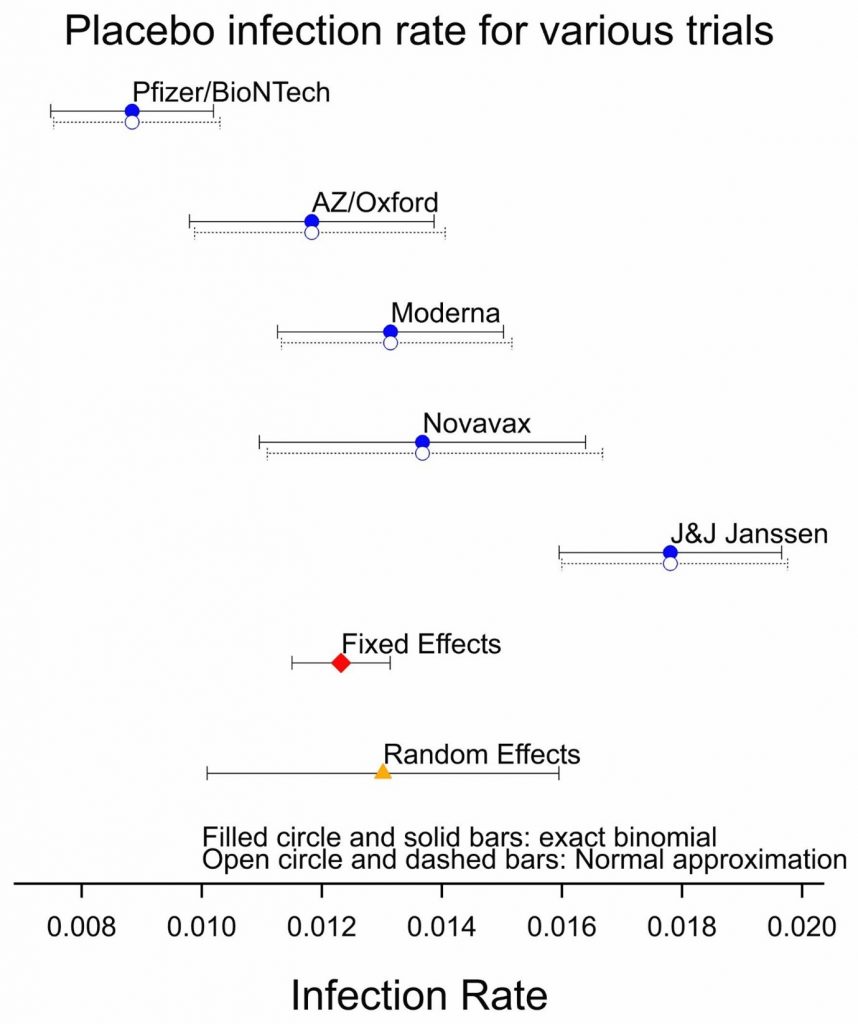
Figure 2: Placebo infection rates for the five studies together with the result of a fixed and random effect meta-analysis.
However, for other matters, we may have no choice. Consider the efficacy of vaccines against new variants of COVID-19. There we may have to use observational studies rather than randomised clinical trials. Figure 2 shows the problem: controls from observational studies are plausibly unreliable in the same way that historical controls would be for a trial. If we calculate the standard errors and the confidence intervals using the statistical approach used for Figure 1, then we are likely to underestimate considerable the uncertainty involved.
What is remarkable about this is how close my simple calculations are to the analyses carried out by the sponsors. There are various technical reasons for this, in particular, that a major source of uncertainty is the number of cases.
The morals are clear. Be very cautious in accepting claims from observational studies. This applies not only to studies of vaccines for COVID-19 but more widely for studies of treatments of infections generally and, indeed, for all studies of treatment efficacy. Observational studies may be relevant for answering some questions when studying antimicrobials and may be unavoidable on occasion, but the statistical methods used to evaluate them run the risk of exaggerating their precision. One should also be wary of using historical controls for antimicrobial trials. Randomised trials using concurrent controls are valuable.
References
- Katella K (2007) Comparing the COVID-19 Vaccines: How Are They Different? Yale Medicine
- Polack FP, Thomas SJ, Kitchin N, Absalon J, Gurtman A, Lockhart S et al. (2020) Safety and Efficacy of the BNT162b2 mRNA Covid-19 Vaccine. New England Journal of Medicine. 383:2603-2615
- AstraZeneca (2021) AZD1222 US Phase III primary analysis confirms safety and efficacy
- Baden LR, El Sahly HM, Essink B, Kotloff K, Frey S, Novak R (2021) Efficacy and Safety of the mRNA-1273 SARS-CoV-2 Vaccine 384:403-416
- Novavax (2021) Novavax Statement on Proof of vaccination for phase 3 clinical trial participants
- U.S. Food & Drug Administration (2021) FDA Briefing Document Janssen Ad26.COV2.S Vaccine for the Prevention of COVID-19
- Senn SJ (2003) Bayesian, likelihood and frequentist approaches to statistics. Applied Clinical Trials. 12(8):35-38.

Stephen Senn is an independent consultant statistician with over 40 years of experience. He frequently writes on topics to do with statistical inference on Deborah Mayo’s Error Statistics Philosophy website and tweets regularly on statistical topics as @stephensenn. Stephen’s main scientific interest has been in the design and analysis of clinical trials, but he has also researched in decision analysis, meta-analysis, ethics and statistical inference. Recently, through his collaboration in the IDeAl project, he has been involved in developing methods for studying treatments for rare diseases. He has also written extensively on the subject of personalized medicine and in particular how the scope for it, although important, may be narrower than many suppose.
Stephen began his career in the National Health Service in England and as a lecturer in Scotland before joining the Swiss pharmaceutical industry in 1987. Since then his interests have been in statistical methods applied to drug development. He has held professorial posts at University College London and the University of Glasgow and most recently was head of the Competence Center for Methodology and Statistics at the Luxembourg of Health. Stephen is the author of more than 300 publications, including three monographs: Cross-over Trials in Clinical Research (Wiley, 1993, 2002), Statistical Issues in Drug Development (Wiley, 1997, 2007) and Dicing with Death (Cambridge, 2003). Stephen is a PhD graduate in statistics from the University of Dundee. He is a recipient of the Bradford Hill Medal of the Royal Statistical Society (2008), the George C Challis medal for Biostatistics of the University of Florida (2001) a Fellow of the Royal Society of Edinburgh and an honorary life member of the International Society for Clinical Biostatistics (ISCB) and Statisticians in the Pharmaceutical Industry (PSI). He is an honorary professor at the University of Sheffield and the University of Edinburgh, both in the UK.
The views and opinions expressed in this article are solely those of the original author(s) and do not necessarily represent those of GARDP, their donors and partners, or other collaborators and contributors. GARDP is not responsible for the content of external sites.